Révisions
TAGs for dummies
Tree Adjoining Grammars (TAGs) have been introduced by Joshi. The basic idea is that complete parse trees can be progressively built by combining elementary trees, using substitution and adjoining.
Elementary trees are formed of initial trees and auxiliary trees.
An initial tree α whose root node R is labeled by syntactic category X may be substituted at a frontier substitution node N of some other tree also labeled by X.
An auxiliary tree β has an unique frontier foot node F sharing a same syntactic label X with its root node. The path from root to foot node is the spine of β. The auxiliary tree β may adjoin on an internal node N of some other tree also labeled X. N is then replaced by β, the subtree rooted at N being attached below the foot node F of β.
We have already mentioned foot and substitution nodes as possible kinds of frontier nodes. Other kinds include lexical nodes to be matched by identical lexical content in the sentence during parsing. Trees with lexical nodes are said to be lexicalized. The grammar is said lexicalized if all trees are lexicalized, which is the case for most TAGs but not an obligation.
The following figure illustrates the use of a few simple elementary tree to derive a complete parse tree for sentence "John sleeps a lot". We observe the substitution of node NP in the tree anchored by sleeps by the tree anchored by John. We then observe the adjoining of the complex adverb "a lot" at the level of the V node. In the present case, we see that adjoining is only adding new node on the right side of the adjoining node V.
.

From a linguistic point of view, TAGs have two main advantages
- an elementary tree provides an extended domain of locality where a single tree may for instance includes a verb and its expected arguments given its valence. For instance, a tree for verb "to give" will cover substitution nodes for a subject argument, a direct object argument, and an indirect prepositional argument introduced by "to" , in relation with the usage frame "someone gives something to someone". The lexical node like a verb that governs a set of expected arguments is said to be the anchor or head of the tree.
- a better handling of so called long distance dependency through the recursive use of adjoining that can insert an arbitrary amount of nodes between two nodes of some elementary trees
From a parsing point of view, an important property of TAGs comes the possibility to parse a sentence of length n with a worst-case complexity in O(n6). For real-life grammars, the complexity is less than that, in particular because they are are mostly TIGs, a restricted subkind of TAGs to be described later.
Decorating trees
Tree nodes may be decorated by feature structures to provide additional morphosyntactic, syntactic, or even semantic constraint. It is for instance possible to ensure agreement constraints in number and gender between a subject and its verb. In first approximation, a feature structure is essentially a set of property=value pairs, where property may denote for instance number, gender, tense, mood, animacy, etc and value may be a variable (to establish constraints between several nodes of a tree) or some specific value generally taken in some finite set of values. For instance, the finite set of values for the gender property is masculine|feminine for French, a possible set of moods for verbs would be infinitive|indicative|participial|gerundive|imperative|... . Some examples of such properties and finite set may be found here and are generally part of the tagset (vocabulary) for a grammar.
For TAGs and because of adjoining, the nodes are actually decorated with a pair (top,bottom) of feature structures. When no adjoining takes place on a node N, the two structures are unified (ie. made equal by binding the variables to values when necessary). When adjoining a tree β on some node N, the top structure to β root node is unified with the top structure of N while the bottom structure of β foot node is unified with the bottom structure of N.
Abstracting trees into tree schema
Many trees have the same structure modulo their lexical anchor. For instance, intransitive verbs will have similar trees, similarly for transitive ones. It is therefore usual to consider tree schema where the anchor node is left underspecified until lexicalized at parsing time by the word found in the sentence.
Organizing tree schema into families
Actually, several tree schema may be related the one to the other through transformations associated to syntactic phenomena. The main such transformation corresponds to the extraction of a verbal argument to build wh-sentences, relative sentences, or even topic sentences. In terms of organization and to ease maintenance, it is therefore interesting to group such tree schema into families.
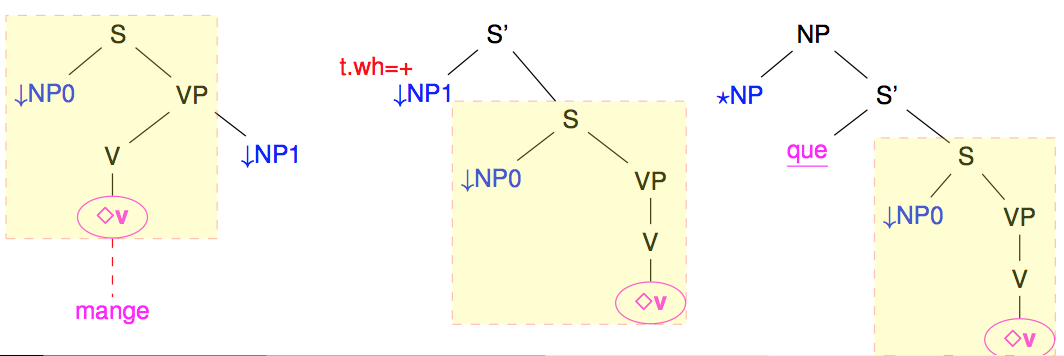
The following figure shows some of the tree schema that belong to the family of the transitive verbs and that be obtained from the left-most "canonical" one to get first a wh version with the extraction of the object NP1 argument and then a relative sentence.
<
p class="align-center">
Families are a nice tentative to organize TAGs. However, as seen in the previous figure, the trees in a same family tend to share large subparts (in yellow). Modifying/correcting one of these trees generally means that all the other trees in the family needs to be also modified. Maintenance becomes relatively complex. Also, because of the number of syntactic transformations, the number of families and trees may grow very quickly. The border between families may also become a bit arbitrary. Should the extraction on the subject argument or the object argument lead to distinct families ? Should intransitive, transitive, di-transitive verbs lead to distinct families, even if they share many subpart of their trees ?
The standard organization model for TAGs (as found in the XTAG grammars developed by Joshi's group at UPenn) leads to very large grammars, with several thousand of trees whose maintenance becomes difficult. Efficiency at parsing time also becomes an issue.
FRMG offers two way to overcome these difficulties:
- sharing descriptive parts through the use of a modular descriptive formalism, namely Meta-Grammars
- sharing subtrees through factorized trees thanks to the use of regexp-like operators
- Version imprimable
- Connectez-vous ou inscrivez-vous pour publier un commentaire
