We have seen that a large coverage TAG may have many trees (several thousand trees, and easily more), but with the elementary trees sharing many fragments. For efficiency reason, it is interesting to reduce the number of trees by factorizing them, sharing the common parts and using regexp-like regular operators to handle the other parts. These regular operators, like the disjunction, does not change the expressive power of the TAGs because they can always be removed by unfactorizing to get a finite set of equivalent non-factorized trees.

Disjunctions

When several subtrees may branch under a same node, we may use a disjunction to group the set of alternatives subtrees. For instance, the following figure shows how several possible realizations of French subjects (as Nominal Phrase, clitics, or infinitive sentences) may be grouped under a disjunction node (noted as a diamond node).

A disjunction to group several alternative realization of subjects

Note: Disjunction nodes are associated with type: alternative in meta-grammar descriptions

Guards

Disjunction may be used to state that a subtree rooted at some node $N$ is present or not. The node is then said to be optional (noted as optional: yes in the metagramar).

However, the presence or absence of a subtree is often controlled by some conditions. Such situations may be captured by guards on nodes, with the conditions being expressing as boolean formula over equations between feature paths (and feature values).

The following figure illustrates the use of a guard over the previous subject disjunction node to state that a subject is present in French when the verb mood is not infinitive, participle, or imperative, and absent otherwise.

A guard to control the presence or absence of a subject

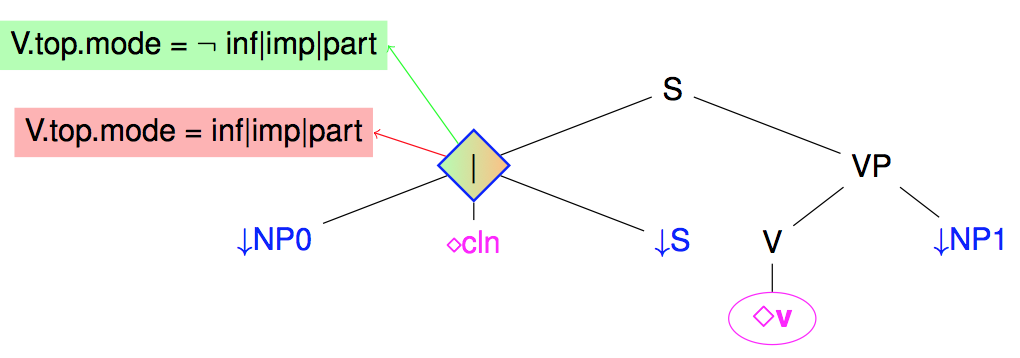
Note: at the level of meta-grammars, the guards are essentially introduced by the => operator on nodes.

For a positive guard on a node $N$ (ie the conditions for its presence) :

N =>     
    V.top.node=value(~inf|imp|part);

For a negative guard on $N$ (ie conditions for its absence), the node must be prefixed by ~

~ N =>     
    V.top.mode = value(inf|imp|part);

A positive (resp. negative) on a node $N$ implicitly implies a true negative (resp, positive) guard, to be then refined by explicit guards. All occurrences of guards on $N$ are accumulated using an AND operator.

It may also be noted that even if a node $N$ is always present, it may be interesting to set up a positive guard on $N$ to represent different alternatives. A special notation may be used for that case and it implicitly sets a fail condition on the absence of $N$ (i.e. the node $N$ can't be absent!)

N +     
    N.top.sat = value(+)     
    |     
    V.top.mode = value(part)     
    ;

Free ordering (shuffling)

Some language are relatively free in terms of ordering of the constituents. This is not really the case for French, but for the placement of post-verbal arguments. Rather than multiplying the number of trees for each possible node ordering, it is possible to use shuffling nodes that allows free ordering between their children.

Free ordering of two post verbal arguments

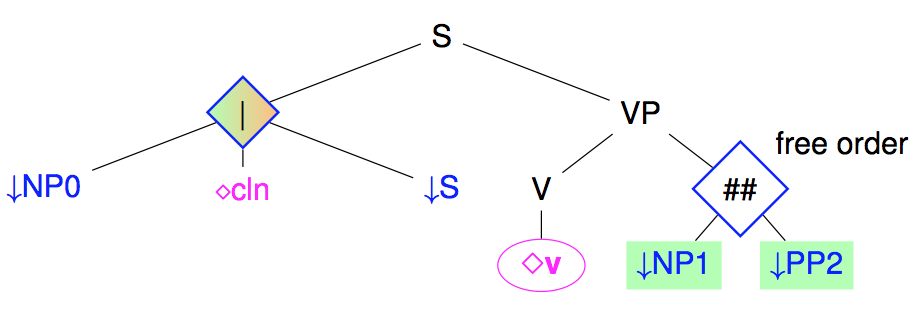
Note: at the level of meta-grammar, there is no need to explicitly introduce shuffle nodes. If the ordering between brother nodes is underspecified given the constraints of the meta-grammar, a shuffle node will be introduced in the generated tree.

Note: The shuffle operator is actually more complex than just presented. It works between sequences of nodes rather than just between nodes, interleaving freely the nodes of different sequences but preserving order in each sequence. For instance, shuffling the two sequences $(A, B)$ with $(N)$ will produce the 3 sequences

• $(A, B, N)$
• $(A, N, B)$
• $(N, A, B)$

If we examine our example tree, we can count how many trees it represents when unfactoring it (assuming guards on subjects and optionality on $NP_1$ and $PP_2$). We actually get $(1_{no\ subj}+3_{subj}) * (1_{no\ args}+2_{1\ arg}+2_{2\ args}) = 20$ trees.

Repetition

The last operator is not used so much in practice and corresponds to the repetition operator $\star$ found in regular expressions. As suggested by its name, it can be used to repeat zero, one or more times some subtree. In FRMG, it is essentially used for representing the iterative part of coordination (, X) between a conjunction of coordination.

A Kleene-star node to represent repetition in coordination

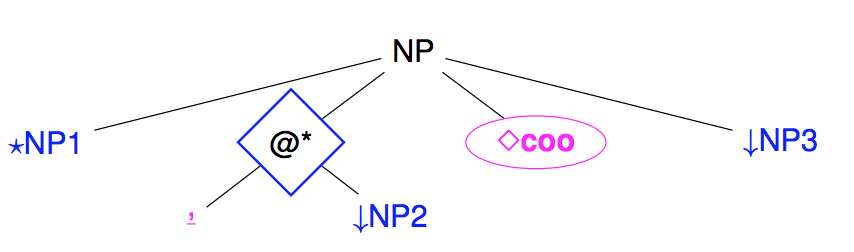
Note: At the level of meta-grammars, repetition is introduced by a node with type: sequence and the special property star: *. This star property is still weakly used but it is planned in some future to specify in a finer way constraints on the number of repetitions (at least one, less than X, more than Y, ...)