The trees of the FRMG grammar that are compiled from the FRMG meta-grammar may be searched and browsed here.

it may also be noted that when using the parsing interface on a sentence, the trees that have been used are listed at the bottom of the right panel.

Some statistics about the grammar

Some statistics about the meta-grammar and the resulting trees (updated September 2016)

The following table confirms the strong compactness of the grammar, with only 381 elementary trees

Distribution by tree types

Classes	Trees	Init. Trees	Aux. Trees	Left Aux.	Right Aux.	Wrap Aux.
415	381	57	324	91	184	49

The following table shows that, surprisingly, the number of tree (schema) anchored by verbs is quite low (only 43 trees), when for other existing TAG grammars, they usually form the largest group. At the difference of most other TAG grammars, one may also note the presence of a large number of non-anchored trees (which doesn't mean they have no lexical nodes, or co-anchor nodes). Actually, most of the trees correspond to auxiliary trees anchored by modifying categories such as adverbs or adjectives. And the main reason why there are so few verbal trees is because it is actually possible to get a very high factorization rate for them. On the other hand, modifiers generally correspond to simple trees that can be adjoined on many different sites (before or a after a verb, between an aux verb and a verb, between arguments, on non verbal categories, ....), a diversity that can't (yet) be captured through factorization.

Distribution by anchors

anchored	v	coo	adv	adj	csu	prep	aux	np	nc	det	pro	not anchored
260	43	50	53	23	10	10	2	3	30	1	7	121

The following table confirms the high compactness for verbal trees, with in particular very few trees needed to cover the phenomena of extraction of verbal arguments (for wh-sentences, relative sentences, clefted sentences, or topicalized sentences). For standard TAG grammars, this is these extraction phenomena that lead to a combinatorial explosion of the number of verbal trees. On the other hand, we observe a relatively high number of auxiliary trees associated to modifiers at sentence levels (adverbs, temporal adverbs, participials, PPs, ...). This is in particular due to the modularity and inheritance properties of meta-grammars that allow us to easily add new kinds of modifiers (and there seems to exist quite a large diversity, yet to be captured :-)

Distribution by syntactic phenomena

canonical	extraction	active	passive	wh	relative	cleft	topic	s-modifiers
8	19	25	10	3	3	7	6	at least 60

The following table shows the heavy use of the factorization operators, in particular of guards. Free ordering is essentially used between arguments of verbs (but also of a few other categories). Repetition is only used for coordinations and enumerations.

Distribution of the factorization operators

guards	disjunctions	free order	repetitions
3713 (+=1916, -=1797)	234	23	57

A study of a complex factorized tree

As mentioned, the most factorized trees are those anchored by verbs (verbal trees) and in particular, the canonical verbal tree (active voice, no extraction). It results from the crossing of 36 terminal classes, which themselves inherit from all their ancestor classes.

The following figure shows a slightly simplified version of this tree.

<

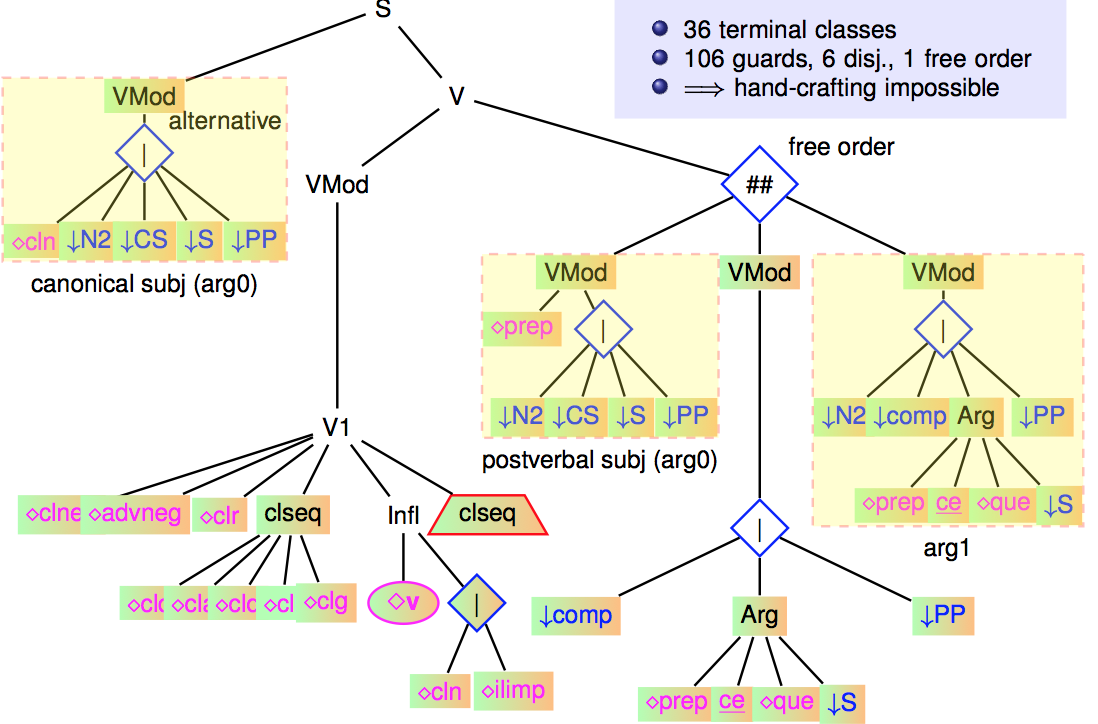
p class="align-center">

Experiments were tried (in 2007) to unfactorize this tree. It led to more that 2 million trees ! Trying partial unfactoring by keeping disjunctions and by filtering out verb categorization frames not found in Lefff lexicon, we get only (!) 5279 trees ! It was possible to parse with the resulting grammar, but it was not possible to exploit all optimizations on it (in particular using a left-corner relation). The grammar was tried on a set of 4k sentences (EasyDev corpus), with the following results:

parser	#trees	avg time (s)	median	90%	99%
+fact -left-corner	207	1.33	0.46	2.63	12.24
-fact -left-corner	5935	1.43	0.44	2.89	14.94
+fact +left-corner	207	0.64	0.16	1.14	6.22

We show that without the left-corner optimization, both version of the grammar (with or without factorization) exhibited similar parsing times (a bit slower for the unfactorized version). However, the left-corner optimization is essential to get much more efficient parsers but is too heavy to be computed over very large grammars.