Révisions
The trees of the FRMG grammar that are compiled from the FRMG meta-grammar may be searched and browsed here.
it may also be noted that when using the parsing interface on a sentence, the trees that have been used are listed at the bottom of the right panel.
Producing the grammar from the meta-grammar
We have a meta-grammar description from one part and we know what kind of trees we wish to get at the end, namely factorized ones. It remains to explain how move from a met-grammar description to factorized trees, through the use of mgcomp, the meta-grammar compiler (implemented on top of DyALog).
There are 3 main steps during this compilation:
- Terminal classes in the meta-grammar hierarchy (i.e. those without subclasses) inherit the constraints of all their ancestor classes.
- Iteratively, starting with the terminal classes, a class C1[−r∪K1] expecting some resource r will be crossed with a class C2[+r∪K2] providing the resource r and the resulting class C[=r∪K1∪K2] will inherit the constraints of both C1 and C2 except for the the resource r that is neutralized (this scheme is slightly more complex for resource under namespaces).
This step stops with a set of neutral classes, i.e. classes that require or provide no resources.
From this set, we consider the subset of the viable neutral classes, i.e. those whose constraints are all satisfiable.
When checking constraints, we also reduce as much as possible guards, by removing trivially true equations, cutting failed alternatives, ... - For each viable neutral class C, we generate a set of minimal (factorized) trees that are compatible with the constraints of C. By minimal, we mean that only nodes mentioned in the constraints of C are used to build trees (and all of them should be used). This generation process is actually relatively complex, in particular to get the shuffling nodes resulting from underspecified orderings between sequences of brother nodes.
Practically, the process of getting a grammar from the meta-grammar involves several conversion of formats and the compilation presented above. It is illustrated by the following figure.
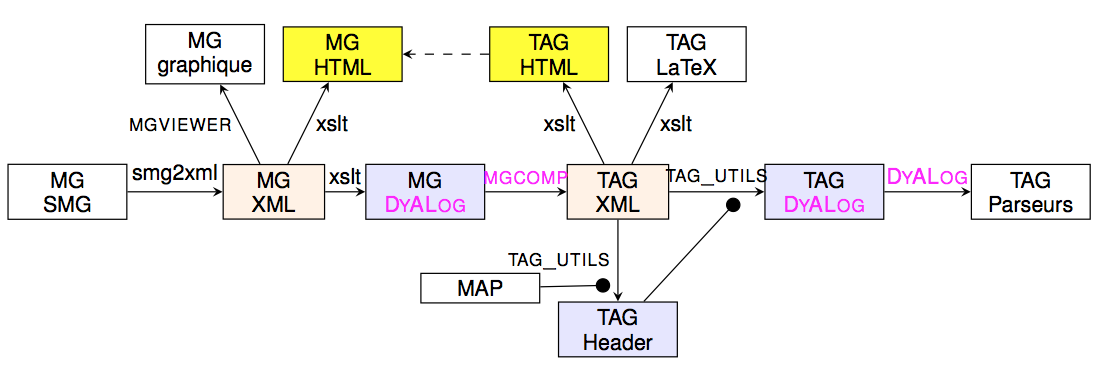
The meta-grammar is written in SMG format, a format more convenient for human writers. It is then converted into XML and then in a Prolog-like format suitable as input for the compiler mgcomp. The resulting grammar is produced in an XML format that may be used to derive several views (including a LaTeX and HTML ones). One of these views is a Prolog-like one that is compiled to get a parser. It is interesting to note that an analysis of the grammar is done to extract a set of features and the sets of values for these features, providing a kind of tagset for the grammar. The process may be eased by directly providing some information through a MAP file. The resulting tagset (seen as an header file) is used during the parser compilation.
Some statistics about the grammar
Some statistics about the meta-grammar and the resulting trees (updated September 2016)
The following table confirms the strong compactness of the grammar, with only 381 elementary trees
| Classes | Trees | Init. Trees | Aux. Trees | Left Aux. | Right Aux. | Wrap Aux. |
|---|---|---|---|---|---|---|
| 415 | 381 | 57 | 324 | 91 | 184 | 49 |
The following table shows that, surprisingly, the number of tree (schema) anchored by verbs is quite low (only 43 trees), when for other existing TAG grammars, they usually form the largest group. At the difference of most other TAG grammars, one may also note the presence of a large number of non-anchored trees (which doesn't mean they have no lexical nodes, or co-anchor nodes). Actually, most of the trees correspond to auxiliary trees anchored by modifying categories such as adverbs or adjectives. And the main reason why there are so few verbal trees is because it is actually possible to get a very high factorization rate for them. On the other hand, modifiers generally correspond to simple trees that can be adjoined on many different sites (before or a after a verb, between an aux verb and a verb, between arguments, on non verbal categories, ....), a diversity that can't (yet) be captured through factorization.
| anchored | v | coo | adv | adj | csu | prep | aux | np | nc | det | pro | not anchored |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 260 | 43 | 50 | 53 | 23 | 10 | 10 | 2 | 3 | 30 | 1 | 7 | 121 |
The following table confirms the high compactness for verbal trees, with in particular very few trees needed to cover the phenomena of extraction of verbal arguments (for wh-sentences, relative sentences, clefted sentences, or topicalized sentences). For standard TAG grammars, this is these extraction phenomena that lead to a combinatorial explosion of the number of verbal trees. On the other hand, we observe a relatively high number of auxiliary trees associated to modifiers at sentence levels (adverbs, temporal adverbs, participials, PPs, ...). This is in particular due to the modularity and inheritance properties of meta-grammars that allow us to easily add new kinds of modifiers (and there seems to exist quite a large diversity, yet to be captured :-)
| canonical | extraction | active | passive | wh-extraction | relative-extraction | cleft-extraction | topic-extraction | sentence-modifiers |
|---|---|---|---|---|---|---|---|---|
| 8 | 19 | 25 | 10 | 3 | 3 | 7 | 6 | at least 60 |
The following table shows the heavy use of the factorization operators, in particular of guards. Free ordering is essentially used between arguments of verbs (but also of a few other categories). Repetition is only used for coordinations and enumerations.
| guards | disjunctions | free order | repetitions |
|---|---|---|---|
| 3713 (pos=1916, neg=1797) | 234 | 23 | 57 |
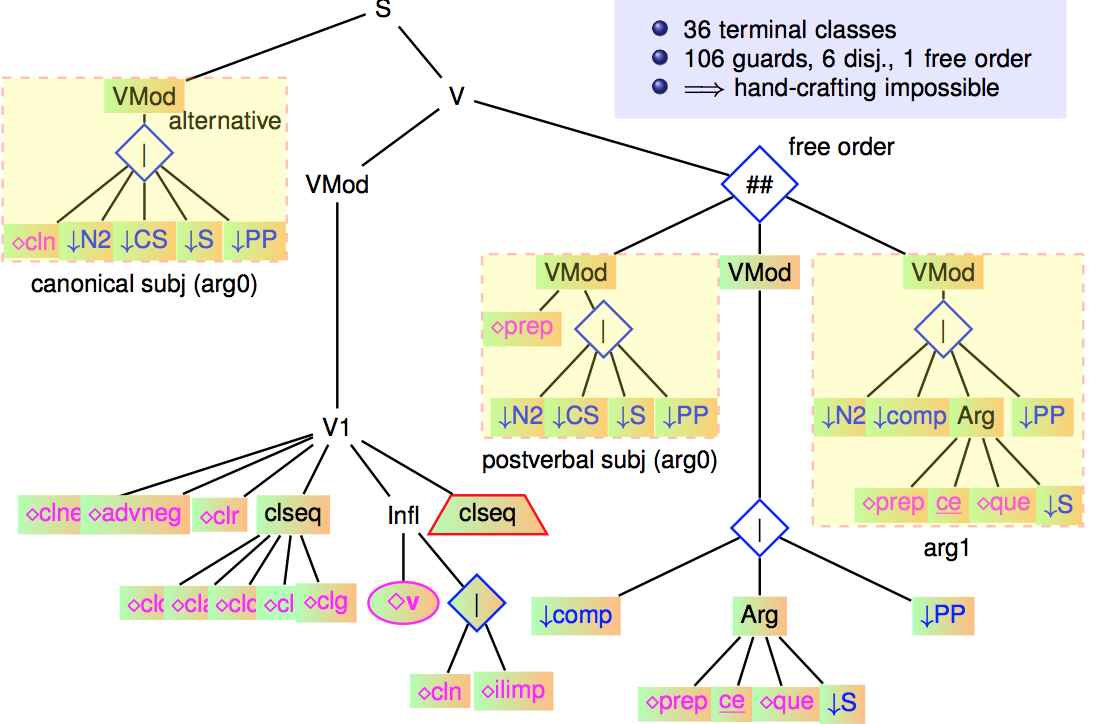
A study of a complex factorized tree
As mentioned, the most factorized trees are those anchored by verbs (verbal trees) and in particular, the canonical verbal tree (active voice, no extraction). It results from the crossing of 36 terminal classes, which themselves inherit from all their ancestor classes.
The following figure shows a slightly simplified version of this tree.
<
p class="align-center">
Experiments were tried (in 2007) to unfactorize this tree. It led to more that 2 million trees ! Trying partial unfactoring by keeping disjunctions and by filtering out verb categorization frames not found in Lefff lexicon, we get only (!) 5279 trees ! It was possible to parse with the resulting grammar, but it was not possible to exploit all optimizations on it (in particular using a left-corner relation). The grammar was tried on a set of 4k sentences (EasyDev corpus), with the following results:
| parser | #trees | avg time (s) | median | 90% | 99% |
|---|---|---|---|---|---|
| +fact -left-corner | 207 | 1.33 | 0.46 | 2.63 |
12.24 |
| -fact -left-corner | 5935 | 1.43 | 0.44 | 2.89 | 14.94 |
| +fact +left-corner | 207 | 0.64 | 0.16 | 1.14 | 6.22 |
We show that without the left-corner optimization, both version of the grammar (with or without factorization) exhibited similar parsing times (a bit slower for the unfactorized version). However, the left-corner optimization is essential to get much more efficient parsers but is too heavy to be computed over very large grammars.
Hypertags
In FRMG, there is no clear notion of tree family and in particular no family of intransitive verbs, transitive verbs or ditransitive verbs. A verbal tree like the one presented above may be anchored by all kinds of verbs, be them intransitive, transitive, ditransitive, with PP args, or with sentential args, ...
So one may wonder how a verb may control the arguments that should be allowed in the verbal tree ?
Actually, each anchored tree τ has an hypertag Hτ (coming from <span style="color:#0000FF;">desc.ht</span>), which is a feature structure providing information in particular about the arguments that are covered by τ. Similarly, a verb v will carry an hypertag Hv build from it lexical information that specifies which kinds of arguments are allowed for v for which realizations. When v is used to anchor τ, its hypertag Hv is unified with Hτ, and the variables present in Hτ will be propagated into τ, in particular in guards.
The following figure shows the unification of the hypertag for the above mentioned trees and the hypertag for verb to promise.
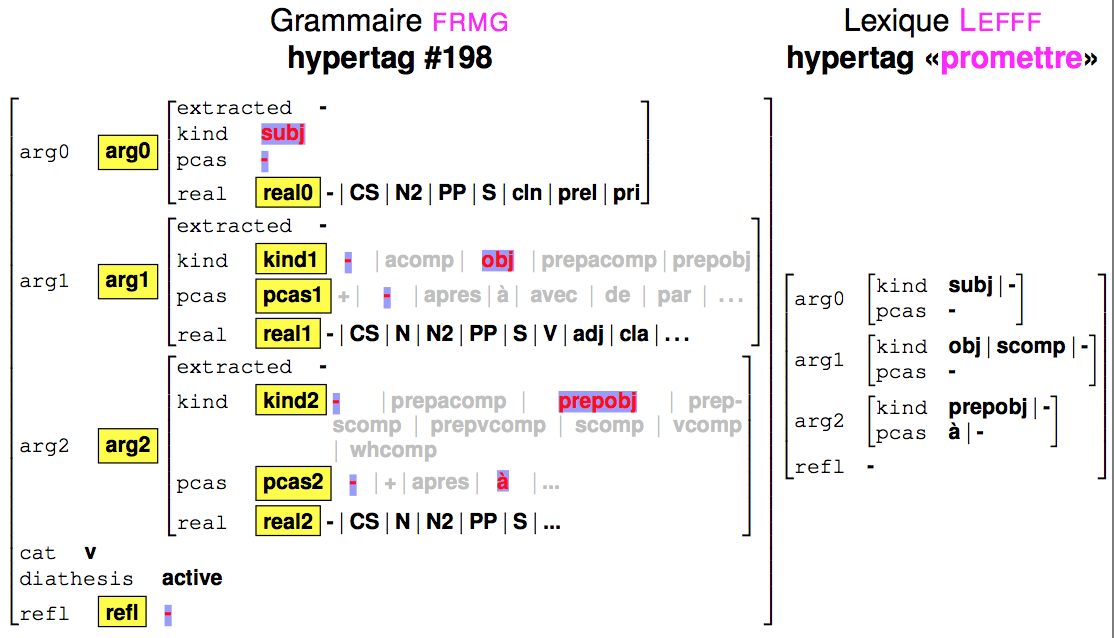
For the anchors, the hypertag information is retrieved from the lexical entries of Lefff lexicon:
- Version imprimable
- Connectez-vous ou inscrivez-vous pour publier un commentaire
